つみたてNISAで月◯万円、年利◯%で運用した場合、20年後の金額がいくらになるかというシミュレーションのツールはよく見かけるのですが、
どのように計算されているのかピンと来ていませんでした。
そこでどのように計算されているのかをちゃんと考えて自分でGoogleスプレッドシートでグラフ化できるようにしてみました。
ここでは次のような例で考えてみます。
- 月2万円つみたて
- 年利1%で運用(複利)
- n年後にいくらになるか?(n=1〜20まで)
年利1%を月利に変換
年利1%で計算しますが、積み立ては毎月2万行うので、月利に変換して考えます。
- 年利 = 月利 × 12
- 月利 = 年利 / 12
年利は月利の12倍です。
月利が1%だったら年利は12%となります。
月利イコールの形に直すと、
月利 = 年利 / 12
となります。
そのため年利1%の場合、月利はどうなるかというと、
月利 = 0.01 / 12
となります。
月2万円、年利1%の場合の20年後の積立金額を計算
汎用性を高めるために文字を使いながら説明していきます。
GとpとtとS(t)を導入します。
- G : 毎月の積立額(今回の場合は2万円です)
- p : 年利(今回の場合は年利1%なので0.01です)
- t : tヶ月後(1〜240までの整数を想定しています)
- S(t) : tヶ月後の積立金額合計
1ヶ月目終わりの積立金額合計
まずは1ヶ月目の場合について考えてみます。
1ヶ月目に2万積み立ててます。(当然ながら)
1ヶ月の終わりには2万円が積み立てられています。
よって、t = 1 の場合、S(t)がどうなるかというと、
となります。シンプルですね。
2ヶ月目終わりの積立金額合計
続いて、2ヶ月目が終わった際の積立金額合計を考えていきます。
ポイントはこちら。
- 2ヶ月目分のG(2万円)を積み立てる←ここに利息はかからない
- 2ヶ月目はじめにG(2万円)が積み立てられている←ここに利息がかかる
これまでの積み立て分に利息がかかっていくので、
2ヶ月目分の積み立て分G(2万円)には利息がかかりませんが、
2ヶ月目がはじまる時点に積み立ててあったG(2万円)には利息がかかります。
さて、2ヶ月目終わりには積立金額の合計はどうなっているか計算してみます。
2ヶ月目から月利の計算がでてきますね。
月利 = 年利 / 12 なので、年利がpだと、月利 = p / 12 と表せます。
2ヶ月目がはじまる時点に積み立ててあったG(2万円)には利息がかかった場合、金額がどうなるかと言うと、
で表せます。
よく消費税を計算するときに税率8%なので、税込価格を知りたいときには税抜価格に1.08をかけますよね。ああいった感じで「1 + p/12 」が出てきます。
さて、2ヶ月後、つまりt = 2 の場合、積み立て金額合計S(t)がどうなるかというと、
となります。
ちょっと難しくなってきたかもしれません。
ちょっときついという方向けに、具体的に数値を入れて計算してみます。
毎月2万円積み立て、年利1%の場合、2ヶ月後の積立合計金額は、
G = 20,000 、 p = 0.01 となるので、
S(2) = 20,000 + 20,000 × ( 1 +0.01 / 12 )
= 40016.6666667
となります。17円くらいプラスになる計算です。
つみたてNISAのシミュレーションツールでも40,017円と表示されるのを確認できると思います。
3ヶ月目終わりの積立金額合計
同様に・・・と済ませたいところですが、まだ3ヶ月目なのでもう少し説明します。
2ヶ月目のときと同じように考えていきましょう。
ポイントはこちら。
- 3ヶ月目に積み立てる分 G ←ここに利息はかからない
- 2ヶ月目に積み立てた分 G ←ここに利息がかかる
- 1ヶ月目に積み立てた分 G × ( 1 + p / 12 ) ←ここに利息がかかる
こうして並べてみるとわかりやすくなってきたのではないでしょうか。
1ヶ月目に積み立てた分の利息のかかる部分は、
G × ( 1 + p / 12 ) となる点がポイントです。
2ヶ月目に利息がかかった部分に対して、さらに利息がかかっていきます。
3ヶ月後、つまりt = 3 の場合、積み立て金額合計S(t)がどうなるかというと、
となります。
nヶ月目終わりの積立金額合計
規則性が見えてきました。
S(1)とS(2)とS(3)を並べてみます。
S(2) = G + G × ( 1 + p / 12 )
S(3) = G + G × ( 1 + p / 12 ) + G × ( 1 + p / 12 ) ( 1 + p / 12 )
となります。
Σ(シグマ)を使って表す
実は、tヶ月後の積立合計金額S(t)は、∑(シグマ)を使って次のように表せます。
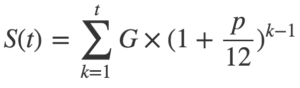
これを計算すれば良いだけになります。
Σ(シグマ)は総和を表します。

上の例では、k=1、2、3、4の場合について代入して和を求めます。
が、しかしこれはいったいどう計算すればよいのでしょう。
等比級数の和の公式が利用できる
この時に必要になるのが等比級数の和の公式です。(これは高校の知識です。なんとなく習ったことは覚えていました。)
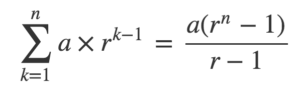
この公式と、先程のS(t)を見比べて、あてはめていくと計算できます。
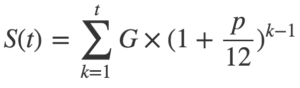
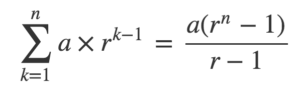
すると、
- a ⇒ G
- r ⇒ (1 + p / 12 )
とすれば良いので、S(t)は以下のように計算できます。
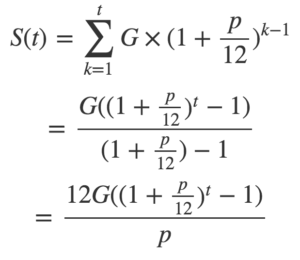
S(t)を、Gとpとtを使って表すことができました。
後は、Gとpとtを代入すれば求まります。
グラフ化の方法の詳細について別の記事で書く予定ですが、グラフ化することで次のようなグラフが作れます。
毎月2万円ずつ20年積み立てた場合の年利ごとの積立金額のグラフ
毎月2万円ずつ、20年積み立てた場合、
- 年利0%
- 年利1%
- 年利3%
- 年利5%
の場合について、積立金額がどうなるかを示したグラフが以下になります。

▲横軸は◯ヶ月、縦軸は積立金額です。
20年積み立てると、年利5%の場合は年利0%の場合に比べて340万円ほどの差になります。
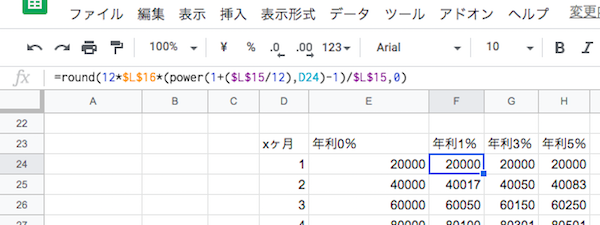
▲参考までに、Googleスプレッドシートで入力する際の計算式です。
